Parameter inference in nonlinear dynamical systems via recurrence plots and convolutional neural networks
Jul 9, 2025·
 ·
0 min read
·
0 min read
Luiza Lober
Equal contribution
,Francisco A. Rodrigues
Equal contribution
,Matheus. S. Palmero
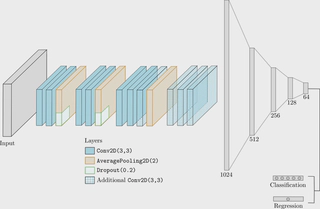 General architecture of the CNN implemented. Layers indicated in solid colors were used for both dynamics, with the hatched blocks employed solely for the dynamics of the Standard map, and dropout used only for the Logistic map.
General architecture of the CNN implemented. Layers indicated in solid colors were used for both dynamics, with the hatched blocks employed solely for the dynamics of the Standard map, and dropout used only for the Logistic map.Abstract
Inferring control parameters in nonlinear dynamical systems is an important task in analyzing general dynamical behaviors, particularly in the presence of inherently deterministic chaos. Traditional approaches often rely on system-specific models and involve heavily parametrized formulations, which can limit their general applicability. In this study, we present a methodology that employs recurrence plots as structured representations of nonlinear trajectories, which are then used to train convolutional neural networks to infer the values of the control parameter associated with the analyzed trajectories. We focus on two representative nonlinear systems, namely, the logistic map and the standard map, and show that our approach enables accurate estimation of the parameters governing their dynamics. When compared to regression models trained directly on raw time-series data, the use of recurrence plots yields significantly more robust results. Although the methodology does not aim to predict future states explicitly, we argue that accurate parameter inference, when combined with predetermined initial conditions, enables the reconstruction of a system’s evolution due to its deterministic nature. These findings highlight the potential of recurrence-based learning frameworks for the automated identification and characterization of nonlinear dynamical behaviors.
Type
Publication
Physical Review E